史云鵬，周棋
（同濟大學水污染控制與資源化研究國家重點實驗室，上海 200092）

　　摘　要：人工濕地是處理污水的一種經濟有效的方法。本文對其污染物去除動力學模型的研究現狀及進展進行了概述，并對其今后發展的趨勢作了展望。
　　關鍵詞：人工濕地；動力學模型；污水處理
　　中圖分類號：X703.1
　　文獻標識碼：A
　　文章編號：1009－2455（200）06－0012－04

Progress of Development of Kinetic Models for Pollutants Removal with Constructed Wetlands
SHI Yun-peng，ZHOU Qi
（State Key Laboratory of Pollution Control and Resource Reuse，Tongji University，Shanghai 200092，China）

　　Abstract：Constructed wetlands provide an economical and effective method for wastewater treatment.Usual　kinetic models for pollutants removal in the treatment of wastewater with constructed wetlands include first－stage　kinetic models and Monod models，both of which are based on the mass balance of pollutants in stable status.In　future，it is also necessary to take into consideration the effects of space distribution of vegitation and actual residence time in improving and developing the mathematic models.
　　Key words： constucted wetlands；kinetic model；wastewater treatment

　　自西德1974年首次建造人工濕地以來，由于其具有投資低、出水水質好、操作簡單、維護和運行費用低等特點，被廣泛用于生活污水^[1-2]、礦山酸性廢水^[3-4]、紡織了業^[5]和石油工業^[6-7]等工業廢水的處理。
　　人工濕地作為一種較新的水處理技術，對其處理機理的理解還不夠充分，對其影響因素的認識還不夠全面，因此經常由于設計不當使得出水達不到設計要求或者不能達標排放，有時人工濕地甚至還會成為污染源””。因此對濕地污染物去除動力學的研究可以為濕地的設計提供進一步的理論支持。
　　本文概要地介紹了人工濕地污水處理的污染物去除動力學模型的研究進展。

1 一級動力學模型

1.1 一級動力學模型簡介
　　濕地設計通常采用的是一級動力學模型，其基本設計方程被澳大利亞^[10]、歐洲^[11]、美國^[12-13]廣泛應用于濕地的設計和對濕地污染物去除效果的預測。雖然有許多局限性，但由于其參數的求解及計算過程都很簡單，因此目前仍把它作為描述濕地中污染物去除的最合適的方程^[14]，廣泛應用于BOD、營養物、SS和細菌以及金屬離子的去除計算。
　　用于濕地的一級動力學方程，主要考慮處理負荷與處理效率之間的關系，模型的推導以基質的降解服從一級反應動力學為基礎。經常《段設模型中的一些參數如速率常數等為常量，與水力負荷或進水濃度無關，以及濕地中的水流形態為穩定的柱塞流等。
　　這些一級動力學模型有的采用體積速率常數kv來確定濕地所需的體積^[15]，有的采用面積速率常數k。來確定濕地所需的面積^[9,16-17]，kv多用于潛流型人工濕地中，而kA則在表面流入工濕地中應用更多。
　　這些一級動力學模型通常的表達方式為^[9]：
　　　　　　　　　c0ciexp（－kv·t） （1）
　　　　　　　　　 c0=ciexp(-kA/q)
　　式中：C_i——進水濃度，[M／L³]；
　　　　　C₀——出水濃度，［M／L³］；
　　　　　kv——體積去除速率常數，［1／T］；
　　　　　kA——面積去除速率常數，［L／T]；
　　　　　t——水力停留時間，[T]；
　　　　　q——水力負荷，［L／T］。
1.2 二參數一級動力學模型
　　上述的一級動力學模型中只包含一個參數kv或k。。在Eckenfelder模型中，如果污染物中存在不可生物降解部分，則需在方程中加人不可生物降解物質濃度項。在濕地中，即使沒有不可降解的污染物，大氣或地下水的貢獻、化學作用以及生物地理化學循環也會產生背景濃度。即使是BOD，由于植物枯葉或其它有機物分解生成BOD，同時內源自養過程積累并將含碳有機物釋放回濕地中，也會形成1－10 mg／L背景 BOD^[14]。于是Kadlec和Knight^[9]建議引入背景濃度，低于背景濃度的污染物不能被降解，并在一級反應動力學方程中加入背景濃度項C*：
　　　　　　　（co—c^*）／（ci—c^*）＝exp（—kv·t）（3）
　　　　　　　（co—c^*）／（ci—c^*）＝exp（—kA／q）（4）
1.3 三參數一級動力學模型
　　不論單參數還是二參數模型，在運行和設計條件改變時，都不能保持參數的穩定性，于是研究者又在模型中加人了第三個參數，提出了三參數模型。
1.3.1 加入描述水力負荷變化對k值影響的參數m，對k值進行修正：
　　　　　　　　kv＝kv′·qm （5）
　　研究表明參數m的引入可以提高數據與模型的吻合程度，但并不能消除水力負荷對表觀背景濃度的影^[18]。
1.3.2 加入表征擴散特性的參數
　　濕地示蹤實驗結果與考慮擴散的二維速度場相類似，所以在方程中加人擴散參數，得到：
　　　　　（co－c*）／ ci－c*）＝［4 beXp（Pe／2）］／
　　　　　［（1＋b）2exp（bPe／2）－（1－6）2 exp（－bPe／2）］　　(7)
　　　　　　b＝(1+4Da/Pe)0.5 （8）

　　式中：Pe—Peclet數（Pe=uL／D），
　　　　　u——流速，[L/T]；
　　　　　D——擴散系數，［L²／T］；
　　　　　 Da—Damkohler數（Da＝kv·t）。
　　擴散參數的加入只能對流動非理性特性中的擴散引起的偏差進行修正，但是對于短流等的影響卻沒有在方程中得到反映。
1.4 一級動力學模型的局限性
1.4.1 參數的不穩定性
　　一個好的模型其所含的參數不應隨操作條件的改變而變化，但單、二、三參數模型都不能滿足對參數穩定性的要求。
　　通常認為速率常數和背景濃度為常數，但實際上它們與濕地的特征及操作條件有關，其值受自由水深、水力負荷、進水濃度。擴散、降雨和蒸發等各種因素的影響^[9,18]。另外一級動力學模型假設速率常數和背景濃度在時間和空間上保持不變，但是由于濕地植被及濕地中微生物的空間分布不均勻，所以必然造成速率常數和背景濃度的空間分布；并且由于一天中氣溫等條件的變化，它們的取值在一天當中也是變化的。
　　所以即使對同一個濕地而言，一組參數也只適用于一組數據，而對另一組數據可能就無效，模型參數不是某個固定的值，而是有個范圍。
1.4.2 非理想流動特性的影響
　　風、生物擾動作用、速度梯度、短流以及水流受到濕地植被阻擋的繞流都使濕地中的流動形態偏離了模型最初的柱塞流假設。
1.4.3 季節的影響
　　為了驗證一級動力學模型是否適用于人工濕地對重金屬的去除，Richard R.Goulet等進行研究，結果表明是否符合一級動力學模型與季節有關。溶解性Zn的去除在春、夏、秋季符合一級動力學，在冬季不符合；而溶解性的Fe、Mn與總Fe、總Mn只在春季符合一級動力學模型^[19]。
　　對于那些處理酸礦廢水的濕地，由于金屬負荷高，Fe、Mn還原作用對去除效果的影響不大，所以仍很好的滿足、級動力學模擬[4，20-21]。
1.4.4 去除能力的限制
　　按照一級動力學，污染物的去除速率r［MT^-1］為：
　　　　　　　　　r=Q.Cin(1-exp(-kv.t) 　　 (8)
　　　　　　　　　r=Q.Cin(1－exp（-kA／q） (9)
　　由上式可知，去除速率隨流量和進水濃度乘積（即進水污染物負荷）的增大而增大，這樣在理論上不存在去除速率的界限。只要進水污染物負荷增加，去除速率可以無限增大，濕地似乎具有無限的去除能力，這顯然與實際情況不符。
1.4.5 隨機事件的影響
　　一些不可預見的隨機事件會對系統產生很大的影響，例如進水流量及濃度的波動、氣候、生物活動和其它生態因素。另外降雨和蒸發在濕地中形成了第二水力負荷，這種附加的負荷有很多方面的影響，例如改變了水力停留時間，混合、擴散、短流以及其它流動特性也因此而發生變化。

2 Monod動力學模型

　　在傳統的污水處理設施和附著型生物處理系統中，可以觀察到隨著進水濃度的增加，反應動力學會從零級變為一級[22]。所以假設濕地中的生物過程與其他的生物系統一樣，符合Monod動力學^[23]：
　　　　dc／dt＝k₀.v[c／K＋c）］（10）
　　　　dc／dz=-k₀.vaε/Q·[c／（K+c）]=［－k0.A／(q.z）］·［c／K+c）］　　（11）
　　式中：k₀，v——零級體積速率常數，［ML^－3T^-1］；
　　　　　k₀，A——零級面積速率常數，［ML^-2T^-1]
　　　　　K——半飽和常數，［ML^－3］；
　　　　　Z——濕地床的長度，［L］；
　　　　　ε——濕地床的孔隙率，［L³L^-3］；
　　　　　a——濕地的橫截面面積，［L²]；
　　　　　Q——流量，［L³T^-1]。
　　對于某一濕地床，其k₀，v和床體積V一定，其所能承受的微生物的最大數量也是一定的，所以其最大去除速率也存在一個上限值，即k₀，v·V。
　　定義了標準化負荷RL（即進水污染物負荷與最大可能去除率的比值）和標準化去除率RR（即濕地床污染物去除率與最大可能去除率的比值）：
　　　　　R_L=ciQ／(k₀，v·V）（12）
　　　　　R_R＝（C_i－c₀）Q／k₀。v·V）　　　（13）
　　標準化負荷與標準化去除率的關系如圖1所示。對于某一固定的進水濃度，開始系統處于一級動力學段，隨著流量的增加其去除速率按相應比例增加；直到進入零級動力學段，這時濕地去除速率達到最大（相對于這一進水濃度），流量再增加，去除速率保持不變，出水濃度會增加。
　　提高進水濃度，可以提高其去除速率，同時與之相對應的最大去除速率也就越大。當進水濃度相對于K趨近于無窮大時，濕地達到了其性能的極限。如果標準負荷R凡＜1，濕地的去除效率為100％，即出水污染物的濃度為零。隨著流量的增大，其去除速率按相應比例增大，與圖中斜率為1 的100％去除效率直線相對應；當標準負荷RL≥ 1，濕地的處理能力達到極限，處于飽和狀態，其去除速率等于最大去除速率同時也是濕地的最大可能去除速率，標準化去除率為1，對應于圖中的絕對最大去除率直線。

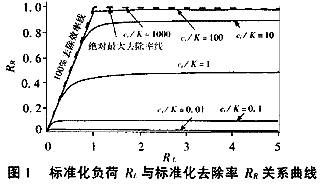
　　與一級動力學模型相比，Monod動力學模型更 符合微生物處理的實際情況，更為合理，所以更適用于那些微生物起主導作用的污染物降解過程。

3 今后研究的方向

　　一級動力學和Monod動力學的設計方程都是 由污染物穩態時的質量平衡得到的，都是濕地床的靜態宏觀模型，兩者都沒有考慮到傳質效率，即都假定物質從液相遷移到生物膜的過程沒有阻力。
　　新的模型應考慮到濕地植被的空間分布，應根據實際的停留時間分布來模擬污染物在濕地中的去除，而不是僅考慮單一的停留時間t。另外人工濕地是一個復雜的生態系統，其對污染物的去除是人工濕地各組成部分共同作用的結果，新的模型應充分考慮到各種因素的影響，因此應對人工濕地污染物去除的機理及其影響因素作深入全面的研究。

參考文獻：

　　[1] Jurgen Ken, Christine Idler. Treatment of domestic and agricul-tural wastewater by reed bed systems[J]. Ecol Eng, 1999,12(1-2):13-25. （1－2）：13－25.
　　[2] L Mandi，K Bouhoum，N Ouazzani.Application of constructed wetlands for domestic wastewater treatment in an arid climate[J]. Wat Sci Tech, 1998,38(1):379-387.
　　[3] K V Heal，C A Salt.Treatment of acidic metal－rich drainage from reclaimed[J].Wat Sci Tech,1999,39(12):141-148
　　[4] william J Mitsch，Karen M Wise Water quality，fate of metals，and predictive model validation of a constructed wetlands treating acid mine drainage[J]. Wat Res，1998，32（6）：1888－1900
　　[5] 李亞治.水葫蘆--水草人工濕地系統在再生漿造紙廢水處理中的應用研究［J］.環境科學動態，2000，（2）：28－30
　　[6] V I Groudeva，S N Groudev，A S Doycheva.Bloremediation of wa ters contaminated with crude oil and toxic heavy metals[j].Int J Miner Process，2001,62（1--4）：293--299
　　[7] Anne L Simi，Cynthia A Mitchell.Design and Hydraulic perfor- mance of a constructed wetland treating oil refinery wastewater[J] Wat Sei Tech，1999，40（3）：301－307
　　[8] StLouis V L，Rudd J W，Kelly C A，et al. Production and loss of methyl menury and loss of total mercury.fron boreal forest catch ments containing different types of wetlands[J].Environ Sci Tech nol，1996，30（9）：2719－2729.
　　［9］Kadlec R H，Knight R L.Treatment wetlands[M].Boca Raton：CRC press，1996
　　［10］Mitchell C，Wise R，Young R，Design of wastewater wetlands In The Constructed wetlands Manual［C］.eds R Young，G white， M Brown，J Burton，B Atkins，2：256－289.Department of Land ＆ Water Conservation，NSW，Sydney，1998.
　　[11] Cooper P F，Job G D，Green M B，et al.Reed beds and constructed wetlands for wastewater treatment［M］.Wiltshire WRc Publications，1996　
　　[12] Reed S C.Subsurface flow constructed wetlands for wastewater treatment：a technology assessment (EPA832-R-93－008）［R］. US Environmental Protection Agency，Washington，DC，1993.
　　[13] Reed S C，Crites R W，Middlebrooks E W Natural systems for waste management and treatment［M］.New York：2nd ed Me GraW－Hill，1998
　　［14］IWA.Constructed wetlands for Pollution control：Processe，Performance, design and operation. Scientific and Technical Report No.8[R]. IWA Publishing. London, UK, 2000.
　　[15]USEPA. Constructed wetlands and aquatic plant systems for municipal wastewater treatment. Design Manual, EPA625/1-88/022[R]. office of research and development, Washington, DC, 1998.
　　[16] Mitsch WJ, Cronk J K, Wu X, et al. Phosphorus retention in constructed freshwater riparian marches[J]. Ecol Appl,1995,5(3):830-845.
　　[17] Upton J, Green M B. A successful strategy for small treatment plants[J].Water Qual Int, 1995,4(2):12-14.
　　[18] Robert H Kadlec. The inadequacy of first-order treatment wetland models[J].Ecol Eng, 2000,15(1-2):105-119.
　　[19] Richard R Goulet, Frances R Pick, Ronald L Droste. Test of the first-order removal model for metal retention in a young construct-et wetland[J]. Ecol Eng,2001,17(4):357-371.
　　[20] Flanagan N E, Mitsch W J, Beach K. Predicting metal retention in a constructed mine drainage wetland[J].Ecol Eng, 1994,3(2):135-372.
　　[21] Tarutis W J, Stark L R, Williams F M. Sizing and performance estimation of coal mine drainage wetlands[J]. Ecol Eng, 1999,12(3-4):353-372.
　　[22] Henze M, Harremoes P, Jansen J C, et al. Wastewater treatment; biological and chemical processes[M].Berlin: Springer,1995.
　　[23]Cynthia Mitchell, Dennis McNevin. Alternative analysis of BOD removal in subsurface flow constructed wetlands employing Monod kinetics[J]. Wat Res, 2001,35(5):1295-1303.

　　作者簡介：史云鵬（1977--），男，黑龍江齊齊哈爾人，現就讀于同濟大學環境科學與工程學院，攻讀水污染控制方向顧士學位，同濟大學94#，電話（021）65985037， spiegeltj@163.com。