復雜供水管網簡化的計算分析
高金良,趙洪賓,陳兵
(哈爾濱工業大學給排水系統研究室)
摘要: 本文提出了一個管網簡化的算法,具有可以適應各種管網拓撲結構、計算結果準確、可任意確定管網簡化程度的特點。經比較管網簡化前后的模型,簡化精度完全滿足管網計算的要求。該算法的實現,為供水系統實時優化調度奠定了堅實基礎。
關鍵詞:復雜管網;簡化;線性模型;非線性模型
Calculation and Analysis of Complex Water Supply Network Simplification
Gao Jinliang, Zhao Hongbin, Chen Bing
(Workgroup of Water & Wastewater System, Harbin Institute of Technology)
Abstract: This paper describes a algorithm of network simplification. It has some advantages that it can adapt many kinds of topology network, get accurate result and determine the extent of network simplification. The precision satisfy the requirement of network calculation by comparing the model of network simplification before and after. We realize the algorithm, so build the stabilized foundation of real-time optimal dispatch in water supply system.
Keywords: complex network; simplification; linear model; non-linear model
一、管網簡化的目的、意義
我國城市配水管網是保證城市居民生活、生產用水的重要市政設施。管網輸送水到千家萬戶,隨著城市的發展,逐漸形成密如蛛網的配水管網。這造成了管網計算分析的極大困難。為此我們必須對極其復雜龐大的配水管網進行簡化。管網簡化的結果主要有三個用途:加速管網平差、得出宏觀管網、實現管網優化調度。
近年來,計算機技術迅猛發展,計算速度迅速提高,普通微機的時鐘頻率已達1GHz。同時管網平差計算在引入了序列分析、壓縮矩陣、有限元等技術后算法計算效率也大大提高。如對有4000個節點,5000條管段的特大城市復雜管網平差,20秒內即可完成。目前可不需要事先進行管網簡化即可實現復雜管網平差模擬計算。同時供水綜合信息系統、管網GIS技術日臻成熟[1],現已不難得出管網的宏觀干線拓撲連接圖形。
但對于管網的優化調度這一重要課題,由于至今對大規模混合離散非線性模型求解十分困難,耗時驚人。優化問題的數學復雜性要遠比管網簡化更大,因此需要簡化后的管網模型,以使得優化調度計算的時間能令人接受。目前,供水系統優化技術應用進展緩慢的一個主要原因是缺少有效的管網簡化方法。故管網簡化對于供水系統計算分析仍是十分必要的。而且由于目前管網簡化的目標單一,不須用于前二個用途,也使得管網簡化算法的考慮可擺脫很多限制,更易于成功實現。
二、管網簡化的現有方法
管網簡化的現有方法主要有:管線省略、合并、分解。
⒈管線省略認為,通常情況下,管徑的大小與管線在供配水中的作用和水力條件的影響成正比。在管網計算允許的范圍內,逐步去掉小管徑的管線,同時對省略管線附近的管線的水力參數進行處理。但需要人為地判斷管線的對管網工作的影響程度(如干線間的小連通管),且不可避免產生計算誤差,尤其對于成環的小管徑的管線很難省略。
⒉在管線合并處理中,并聯、串聯管線的合并在理論上可以得到精確的計算結果,在大中城市的給水管網中,有30%的管線可以做此簡化處理。此外平行管線合并和管線省略一樣需要考慮對其四周管線的處理,有一定誤差。
⒊管網分解是當一個供水區域僅由少數幾條管線供水和其他管網相連時,可以將連接的管線斷開,將一個管網分解為兩個獨立的管網,對兩個管網分別單獨計算。這在連接管線的流向和流量易于確定的時候可以分解,但在大多數管網成環布置、多處連接的情況下難以實現。
三、管網簡化的理論
對于給水管網,節點和管段之間關聯可以由關聯矩陣Λ來表示。矩陣的每行對應著每一個節點n=1,2,Λ,N;每列對應著每一條管段j=1,2,Λ,J。。在矩陣Λ中,每一列僅有二個非零元1、-1,分別對應于該管段的起始和終止節點,其余元素為0;每一行有1、-1,分別對應于流入和流出該節點的管段。則給水管網的水頭損失方程;連續性方程和能量方程可表示為:
q=q(△h)=g│△h│0.54sign(△h)......................(1)
qnod=Λq............................................(2)
△h=ΛTh............................................(3)
q=Q(△h)............................................(4)
其中,q-----管段流量向量;
△h-----管段水頭損失;
g-----管段關聯系數,由管長、管徑、阻力系數確定;
qnod------節點流量向量;
h-----節點水壓向量;
Q(△h)-----向量函數,Q(△h)=(q1(△h1),Λ,qj(△hJ))T。
由⑵⑶⑷式可得,
ΛQ(ΛTh)=qnod.....................................(5)
⒈管網模型線形化
將⑸式線性化對△h求導可得,
Λ(dQ/dΔh)ΛT×δh=δqnod...........................(6)
式中,設A=Λ(dQ/dΔh)ΛT,此矩陣為雅可比矩陣。
且有![]() 。則A可得,
。則A可得,
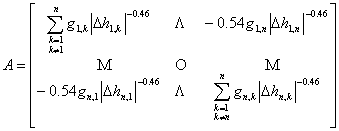 ........⑺
........⑺
⒉化簡線形化模型
對⑺式可以多次重復應用高斯約當消去過程。如將矩陣中消去前r行,即從管網模型中簡化掉r個節點。得新的簡化后的模型可寫為,
 ........⑻
........⑻
對節點流量q也作相應處理。
⒊化簡后模型恢復為非線形模型
經過高斯約當消去過程,得到了化簡后的管網模型A(r)。新的矩陣A(r)包含了原有線形模型的全部特性,即形成了一個新的管段聯系的新管網模型。其管段關聯系數g為,
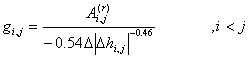 ........⑼
........⑼
對于新的管網模型,可假定新生成的管段的阻力系數C值為100,管長等于管徑,來生成實際具有物理意義的管段。這就得到了新的簡化后的非線性的管網模型。
該管網簡化過程的物理解釋是,通過高斯約當消去刪除一部分原有的管段,合成新的管段中保存了原有管段間的關聯。簡化的非線形模型很好的保留了原始模型的特性。該方法雖然是通過在一個確定的工況點求導來線性化模型,但在一個很寬的管網工作運行條件范圍內,模型的精度完全可以滿足要求。
四、管網簡化的實現
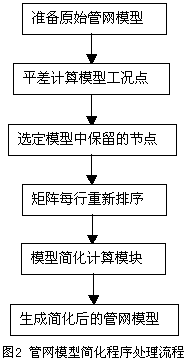
對上述化簡理論過程的實現如圖1所示,化簡程序如圖2所示。
五、應用實例及結論
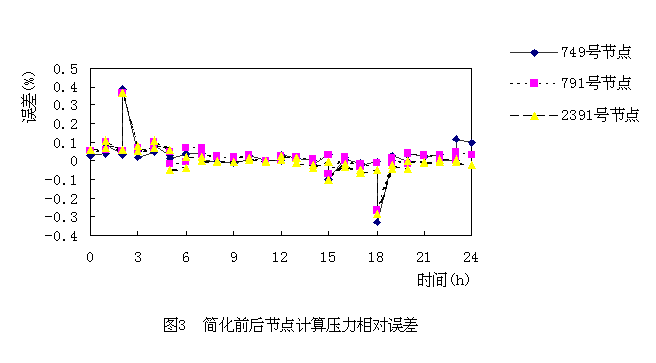
應用上述管網簡化理論,以北方某特大城市實際復雜管網為例進行管網模型簡化計算。該原始管網模型共有3439個節點,4514條管段,3個供水水源。按第12個時段的運行工況點進行簡化計算,去除了3407個節點,形成了僅有32個節點(其中包括10個水源節點), 422條管段的新管網模型。限于篇幅,簡化前后的管網圖省略。通過對簡化前后的管網模型進行平差模擬計算,發現簡化過程對管網計算的誤差影響很小。部分節點、管段的誤差分析見圖3、4。
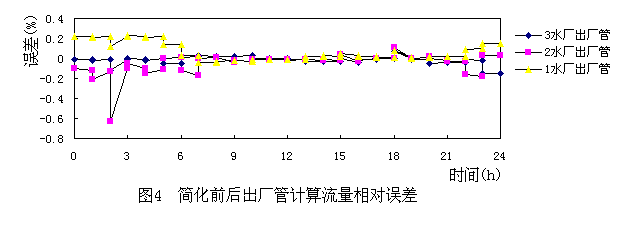
本文提出的管網簡化算法,由于是程序自動處理,可以適應各種拓撲結構、復雜程度的供水管網,可任意確定管網簡化程度,在簡化的過程中不需用戶任何干預處理,簡化精度完全滿足管網計算的要求。管網經過簡化后,可大大減少供水管網優化調度計算的耗時,克服了實現管網優化調度實時性差的難題。
參考文獻:
給水管網理論和計算 中國建筑工業出版社 嚴煦世、趙洪賓
作者簡介:
高金良. 男 講師 哈爾濱工業大學市政環境工程學院
通 訊 處:0451-6282281 150090 哈爾濱工業大學(二區)624#信箱
Email: gaojinliang@mail.hrbucea.edu.cn
論文搜索
發表時間 至
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








